Neuronale Netzwerke komprimieren

Als ich mich um eine PhD-Position beworben habe, wollte ich dem Professor einen Grund geben, mich anzuheuern – also habe ich eine meiner Ideen umgesetzt. Ich vermutete, dass die Gewichte neuronaler Netzwerke zu dicht sind. Es gibt viel Redundanz. Die konventionelle Methode zur Reduktion der Komplexität besteht darin, einen Engpass in die Architektur des neuronalen Netzwerks einzuführen. Das ist jedoch eine ressourcenintensive Lösung. Anstatt die Anzahl der Gewichte zu reduzieren, erhöhen wir sie. Eine weitere Möglichkeit, die Komplexität eines Modells zu reduzieren, besteht darin, die Präzision der Gewichte zu senken, z.B. von 32-Bit auf 8-Bit. Das ist ein legitimer Ansatz, aber wenig inspirierend. Und es ist schwer zu glauben, dass das der einzige und richtige Weg für alle Situationen ist.

Meine Hypothese war, die Gewichtsmatrix mit einem gängigen Algorithmus wie JPEG zu komprimieren. Ich nahm MNIST und trainierte ein kleines CNN:

hidden_layer_size = 512
linear1 = torch.nn.Linear(784, hidden_layer_size, bias=True)
linear2 = torch.nn.Linear(hidden_layer_size, 10, bias=True)
relu = torch.nn.ReLU()

model = torch.nn.Sequential(linear1, relu, linear2)

Die Grösse von 512 für die Hidden Layers war die erste Zweierpotenz, die gute Ergebnisse lieferte.

Die 784 stammt aus der Eingabegrösse, die 28 × 28 beträgt.

Die Hidden Layer ist somit eine Liste von 512 verschiedenen 28 × 28 Matrizen.

Ich nahm jede Matrix und komprimierte sie mit JPEG auf eine Qualität von nur 20%, verlor also viele Informationen, wie hier zu sehen:

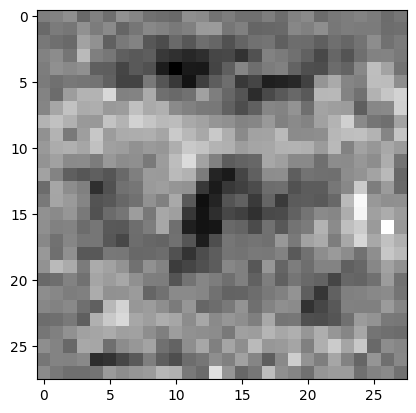Zufällige unkomprimierte Gewichtsschicht

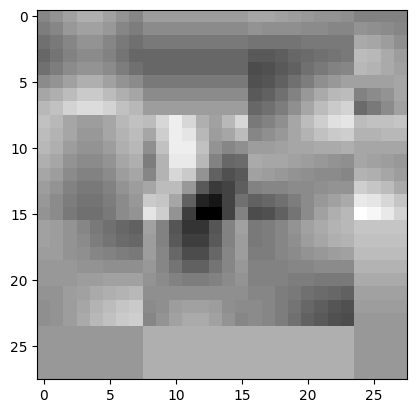JPEG komprimiert 20% Qualität Dieselbe Gewichtsschicht, aber mit JPEG komprimiert

Die Test-Accuracy sank nur von 97% auf 96%, was angesichts der geringeren Auflösung im latenten Raum bemerkenswert ist.

Die Gewichte in einem CNN sind sehr redundant. Mit einem naiven Algorithmus wie JPEG können wir die Dimensionalität deutlich reduzieren. Für die Vorwärtspropagation im Netzwerk brauche ich jedoch die Matrixversion von JPEG, die keinen Speicher spart. Die komprimierten Gewichte könnten verwendet werden, um sie über ein Netzwerk mit geringer Bandbreite wie das Internet zu übertragen. Wir können jedoch einige fundierte Annahmen treffen:

Die Wahl einer anderen Basis für die Gewichte, etwa die Fourier-Basis, anstatt ein unabhängiges Gewicht an jeder Position, könnte die Erstellung grosser Netzwerke mit einer begrenzten Anzahl von Gewichten ermöglichen.
Diese Methode könnte auch in tiefen neuronalen Netzwerken funktionieren.
Die Entwicklung einer differenzierbaren Methode, die mit wenigen Parametern erhebliche Komplexität erzeugt, könnte die Rechenfähigkeiten bestehender Hardware verbessern.