Compressing Neural Networks

When I applied for a PhD position, I wanted to give the professor a reason to hire me, so I implemented one of my ideas. I suspected that the weights of neural networks are too dense. There is a lot of redundancy. The conventional method to reduce complexity is to introduce a bottleneck in the architecture of the neural network. However, this is a resource-intensive way to solve the problem. Instead of reducing the number of weights, we increase them. Another way to reduce the complexity of a model is to lower the precision of the weights, e.g., from 32-bit to 8-bit. This is a legitimate approach but uninspired. And it's hard to believe that this is the only and correct way for all situations.

My hypothesis was to compress the weight matrix using a common algorithm like JPEG. I took MNIST and trained a small CNN:

hidden_layer_size = 512
linear1 = torch.nn.Linear(784, hidden_layer_size, bias=True)
linear2 = torch.nn.Linear(hidden_layer_size, 10, bias=True)
relu = torch.nn.ReLU()

model = torch.nn.Sequential(linear1, relu, linear2)

The size of 512 for the hidden layers was the first power of two that yielded good results.

The 784 comes from the input size, which is 28 × 28.

The hidden layer is thus a list of 512 different 28 × 28 matrices.

I took each matrix and compressed it with JPEG to a quality of only 20%, losing a lot of information, as seen here:

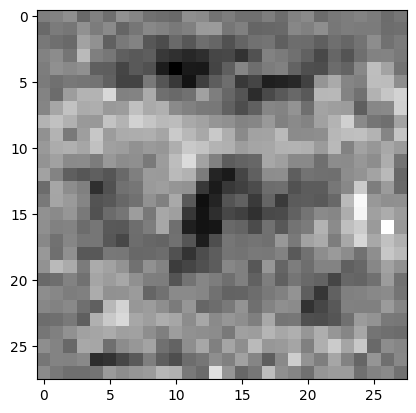Random uncompressed weight layer

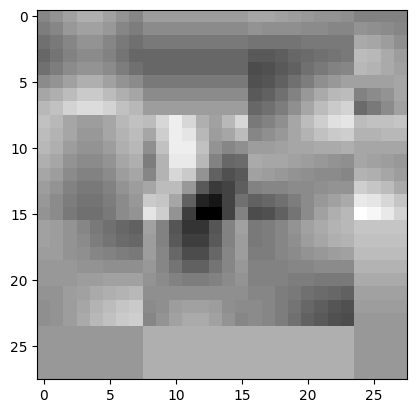JPEG compressed 20% quality Same weight layer but with jpeg compressed

The test accuracy dropped only from 97% to 96%, which is remarkable given the lower resolution in the latent space.

The weights in a CNN are highly redundant. We can significantly reduce dimensionality using a naive algorithm like JPEG. However, for forward propagation in the network, I need the matrix version of JPEG, which does not save memory. The compressed weights could be used to transmit them over a low-bandwidth network like the Internet. However, we can make some informed assumptions:

Choosing a different basis for the weights, such as the Fourier basis, instead of having an independent weight at each position, could enable the creation of large networks with a limited number of weights.
This method could also work in deep neural networks.
Developing a differentiable method that generates significant complexity with few parameters could enhance the computational capabilities of existing hardware.